Creating custom bootstrap tests

Background

p-values can be computed by inverting the corresponding confidence intervals, as described in Section 14.2 of Thulin (2024) and Section 3.12 in Hall (1992). This package contains functions for computing bootstrap p-values in this way. The approach relies on the fact that:

• The p-value of the two-sided test for the parameter theta is the smallest alpha such that theta is not contained in the corresponding 1-alpha confidence interval,
• For a test of the parameter theta with significance level alpha, the set of values of theta that aren’t rejected by the two-sided test (when used as the null hypothesis) is a 1-alpha confidence interval for theta.

Custom hypothesis tests

Bootstrap p-values for hypothesis tests based on boot objects can be obtained using the boot.pval function. The example below, based in part on code from Section 7.4.2 of Modern Statistics with R, shows how to implement a bootstrap correlation test.

First, we create a function for computing the correlation given a bivariate dataset and a vector containing row numbers (the indices of the bootstrap sample). We also include a method option to allow the user to choose which type of correlation is used:

cor_boot <- function(data, row_numbers, method = "pearson")
{ 
    # Obtain the bootstrap sample:
    sample <- data[row_numbers,]
    
    # Compute and return the statistic for the bootstrap sample:
    return(cor(sample[[1]], sample[[2]], method = method))
}

Let’s say that we wish to test the correlation between the variables hp and drat in the mtcars data:

mtcars |> plot(hp ~ drat, data = _)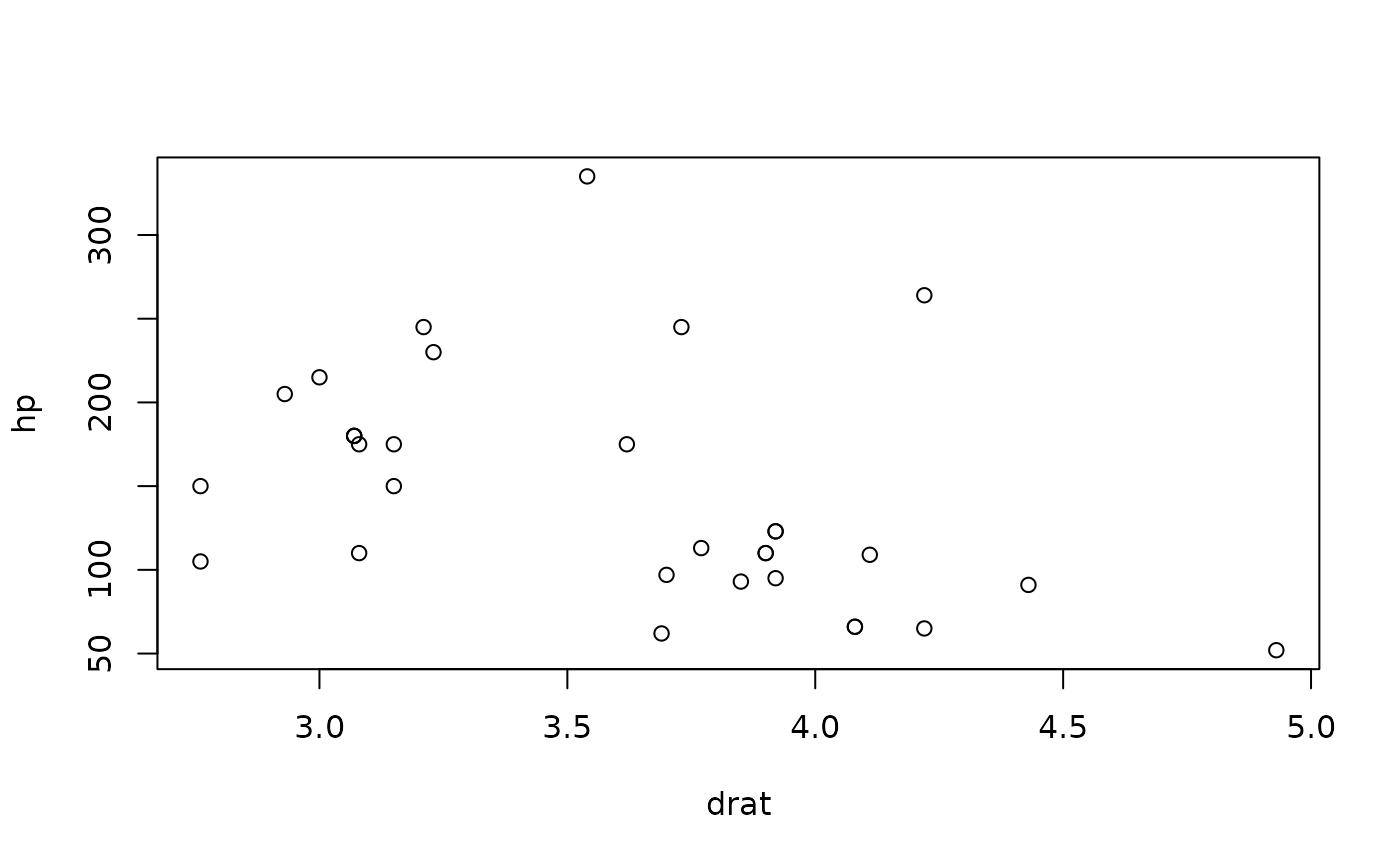

We subset the data (below I use the base R function subset for this; see my post on base R replacements of tidyverse functions for more on this) and then use boot to draw 999 bootstrap samples:

library(boot)
boot_res <- mtcars |> 
              subset(select = c(hp, drat)) |> 
              boot(statistic = cor_boot,
                   R = 999)

If we like, we can plot the bootstrap distribution:

plot(boot_res)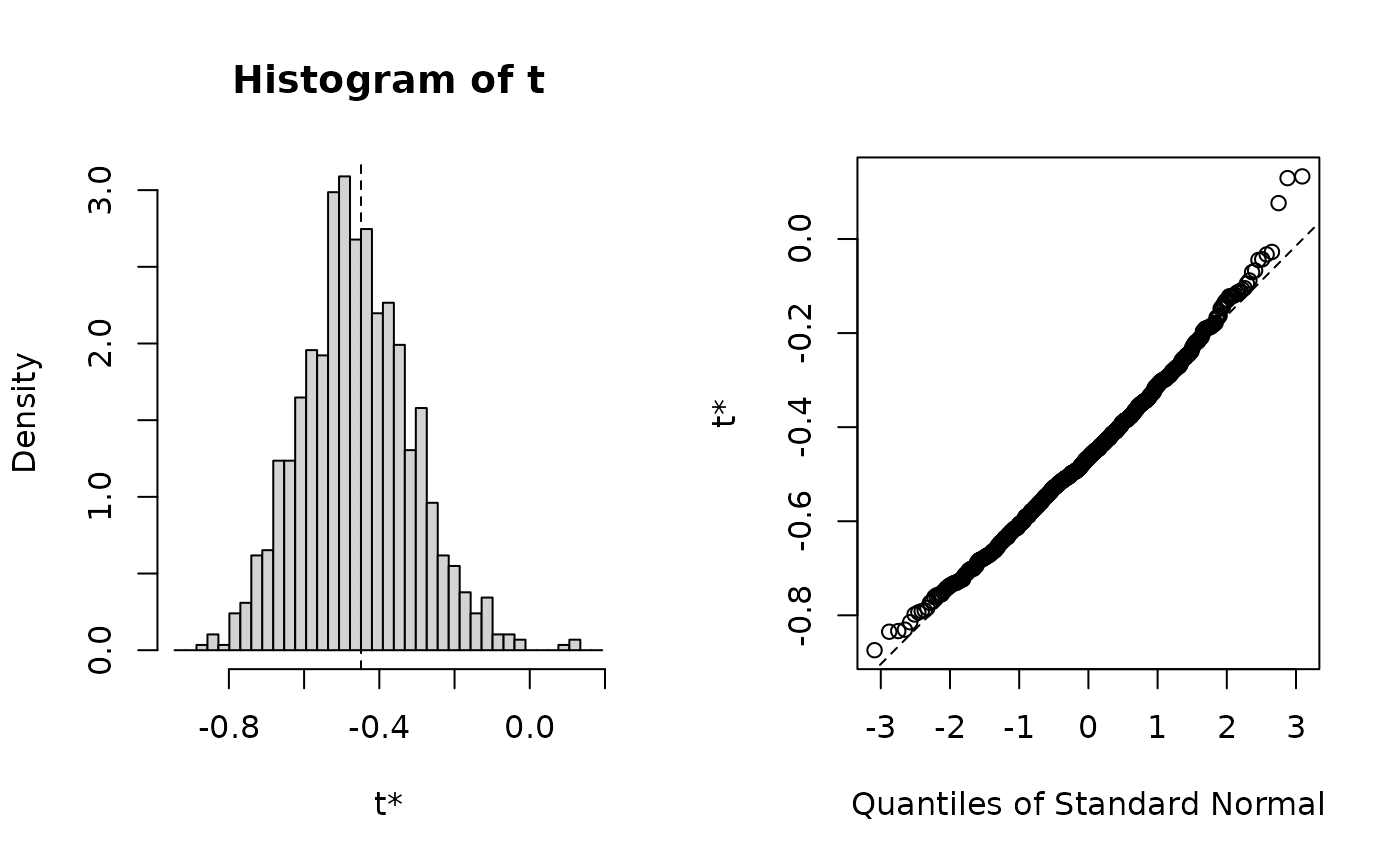

And compute confidence intervals:

boot.ci(boot_res)
#> Warning in boot.ci(boot_res): bootstrap variances needed for studentized
#> intervals
#> BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
#> Based on 999 bootstrap replicates
#> 
#> CALL : 
#> boot.ci(boot.out = boot_res)
#> 
#> Intervals : 
#> Level      Normal              Basic         
#> 95%   (-0.7289, -0.1479 )   (-0.7599, -0.1645 )  
#> 
#> Level     Percentile            BCa          
#> 95%   (-0.7330, -0.1376 )   (-0.6819, -0.0458 )  
#> Calculations and Intervals on Original Scale
#> Some BCa intervals may be unstable

To compute the p-value corresponding to the different intervals, we can now use boot.pval:

# Compute the bootstrap p-value based on the percentile interval:
library(boot.pval)
boot.pval(boot_res, type = "perc")
#> [1] 0.008008008

For studentized intervals, we also need to estimate the variance of the statistic, e.g. using an inner bootstrap. We create a new function for this, run a new resampling, and compute the studentized p-value:

cor_boot_student <- function(data, row_numbers, method = "pearson")
{ 
    sample <- data[row_numbers,]
    
    correlation <- cor(sample[[1]], sample[[2]], method = method)
    
    inner_boot <- boot(sample, cor_boot, 100)
    variance <- var(inner_boot$t)

    return(c(correlation, variance))
}

# Run the resampling:
boot_res <- mtcars |> 
              subset(select = c(hp, drat)) |> 
              boot(cor_boot_student, 999)

# Compute the bootstrap p-value based on the studentized interval:
boot.pval(boot_res, type = "stud")
#> [1] 0.06306306

That’s all there is to it! Note that using boot.pval is completely analogous to how we use boot.ci from boot.

An example from boot

The following example is an extensions of that given in the documentation for boot::boot:

# Hypothesis test for the city data
# H0: ratio = 1.4
ratio <- function(d, w) sum(d$x * w)/sum(d$u * w)
city.boot <- boot(city, ratio, R = 999, stype = "w", sim = "ordinary")
boot.pval(city.boot, theta_null = 1.4)
#> [1] 0.4874875

# Studentized test for the two sample difference of means problem
# using the final two series of the gravity data.
diff.means <- function(d, f)
{
  n <- nrow(d)
  gp1 <- 1:table(as.numeric(d$series))[1]
  m1 <- sum(d[gp1,1] * f[gp1])/sum(f[gp1])
  m2 <- sum(d[-gp1,1] * f[-gp1])/sum(f[-gp1])
  ss1 <- sum(d[gp1,1]^2 * f[gp1]) - (m1 *  m1 * sum(f[gp1]))
  ss2 <- sum(d[-gp1,1]^2 * f[-gp1]) - (m2 *  m2 * sum(f[-gp1]))
  c(m1 - m2, (ss1 + ss2)/(sum(f) - 2))
}
grav1 <- gravity[as.numeric(gravity[,2]) >= 7, ]
grav1.boot <- boot(grav1, diff.means, R = 999, stype = "f",
                   strata = grav1[ ,2])
boot.pval(grav1.boot, type = "stud", theta_null = 0)
#> [1] 0.04904905

References

• Davison, A.C. and Hinkley, D.V. (1997) Bootstrap Methods and Their Application. Cambridge University Press.
• Hall P (1992). The Bootstrap and Edgeworth Expansion. Springer, New York.
• Thulin, M. (2024) Modern Statistics with R. Second edition. Chapman & Hall/CRC Press.